The View on Different Dimensions

Physics

Click to watch the summary of this article

An object's dimension, as defined in physics and mathematics, represents the minimum number of coordinates needed to specify any point within it. Depth perception, also known as 3D perception, is a capability of the human eye. Individuals with this ability perceive the world in all three spatial dimensions. Initially, the visual cortex of each human eye interprets the three dimensions of space as two-dimensional (2D) images. However, a question arises: if we can observe only three dimensions, could there be more? Mathematical theory may suggest a fourth dimension, according to theoretical physicists. Yet, there remains the tantalizing possibility of numerous dimensions existing within the universe. String theory, one of the most influential physics models of the past fifty years, proposes that the universe operates in ten dimensions. This article aims to explore our current knowledge about various dimensions.

The 2D dimension, often referred to as two-dimensional space, is a fundamental concept in mathematics and physics that represents a plane where points are located using two coordinates—typically denoted as x and y. Shapes, figures, and objects lack depth in this domain, existing solely in length and width without height. This flatness characterizes drawings, graphs, and geometric structures. Ranging from simple shapes like squares and circles to intricate diagrams and artworks, the 2D dimension serves as a foundational element for comprehending spatial relationships, design, and various mathematical principles. It holds significance in fields spanning from art and architecture to computer graphics and scientific modeling.

In mathematics and science, the 2D dimension defines a geometric space with only two directions—commonly depicted by horizontal and vertical axes or coordinates. Objects in this two-dimensional realm possess length and width but lack depth or thickness. This domain encompasses fundamental shapes such as squares, triangles, circles, and rectangles. Two-dimensional representations serve to convey information in graphs, charts, and maps.

The 2D dimension is crucial for understanding concepts like vectors, matrices, transformations, and coordinate geometry. It acts as a stepping stone for exploring more intricate spatial dimensions, serving as a foundational platform for many higher-dimensional constructions and theories. Moreover, in computer science and graphics, the 2D dimension is employed for generating images, constructing user interfaces, and creating visual simulations.

3D (three-dimensionality) constitutes a space comprising three spatial dimensions: length, width, and depth. Our world and every object within it encompass all these three dimensions. While some individuals argue that we live in four dimensions and that the fourth dimension is time, it's generally accepted that we inhabit a three-dimensional world. Furthermore, our eyes possess stereoscopic vision, enabling recognition and processing of images that consist of three dimensions.

Three dimensions represent the maximum number of dimensions detectable by the human eye. This limitation prevents us from seeing more than three dimensions and recognizing them. Our eyes lack the capability to perceive objects beyond three dimensions. To comprehend this limitation better, one might reference Edwin Abbott Abbott's satirical novel "Flatland: A Romance of Many Dimensions" (1884). In this narrative, geometric figures inhabit a 2D world resembling a sheet of paper. Figures in this world can only recognize two dimensions: length and width. The protagonist, a Pentagon, encounters a sphere from a 3D world. Initially, the Pentagon fails to recognize the sphere as a 3D object and considers it a 3D object. However, later on, the Pentagon realizes the existence of more than two dimensions. Despite this understanding, when the Pentagon attempts to explain 3-dimensionality to other figures, they remain unconvinced due to their incapacity to perceive all three dimensions simultaneously.

This limitation likely explains why we cannot discover or imagine the fourth or higher dimensions. Our eyes are incapable of recognizing dimensions beyond three, just as creatures dwelling in a 2D world cannot recognize the third dimension, similarly, humans inhabiting a 3D world cannot perceive more than three dimensions.

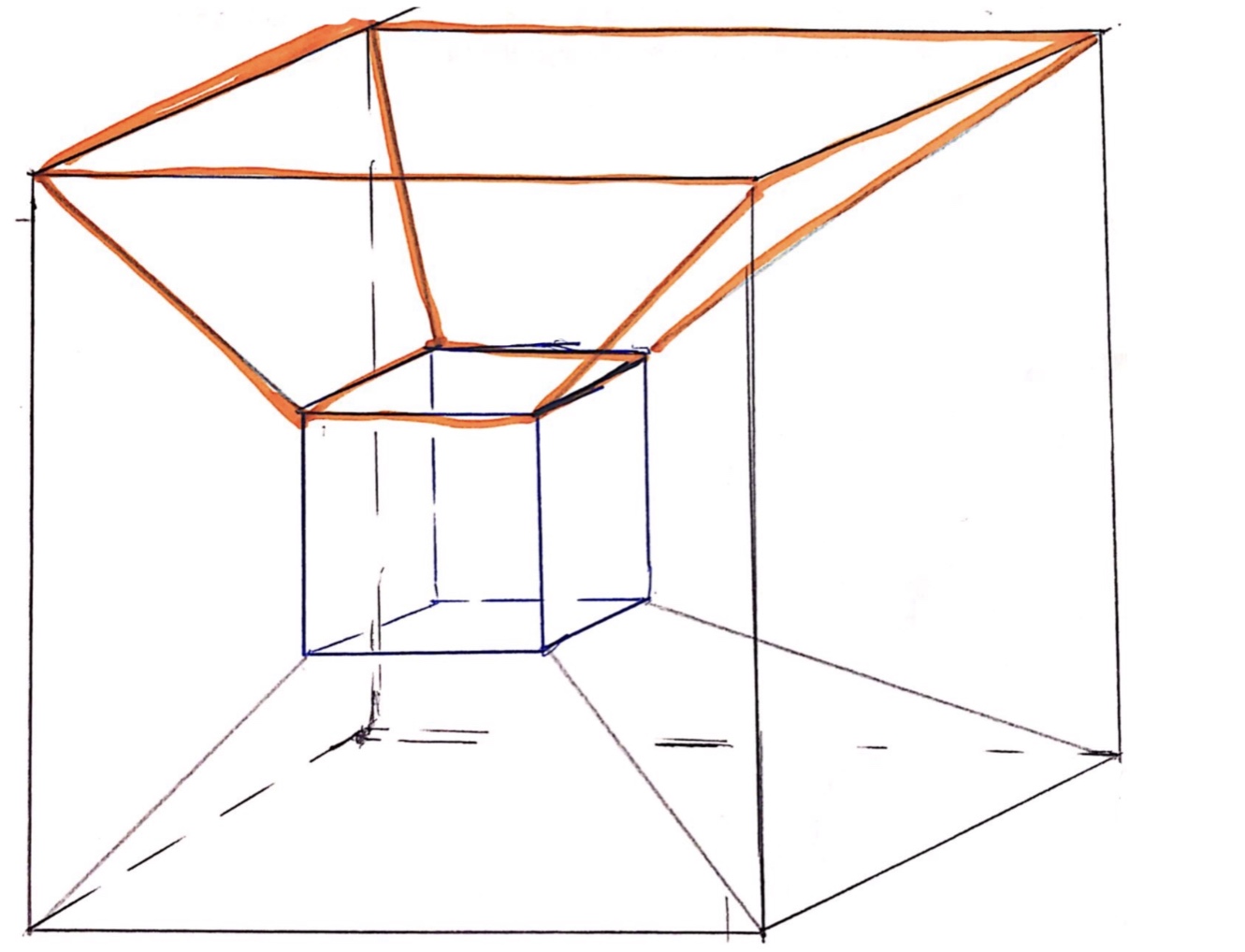
The fourth dimension is one of the most discussed dimensions among the total of 11. For instance, a 4D cube is an example—a 2D model representing a 3D model of a 4D cube. To conceptualize a 4D cube, one needs to extend the cube in a direction perpendicular to its first three dimensions. However, residing in a three-dimensional space renders this extension impossible for us. Described by four numbers—x, y, z, and w—the four-dimensional cube retains properties of its 3D version, notably, all angles being 90 degrees, and all sides possessing equal length. While various four-dimensional objects have distinct names, sizes, and angles, the figure denoted as a cube with four dimensions is referred to as a tesseract.

We can represent any dimension in terms of another dimension. In essence:

One dimension consists of an infinite number of 0-dimensional points.

A two-dimensional plane comprises an infinite number of stacked lines.

Our three-dimensional world encompasses an infinite number of stacked planes.

Hence, we may infer that the 4D realm constitutes an infinite collection of 3D worlds. Consequently, as we move within our three-dimensional world, this infinite array of worlds remains part of our existence.

It's crucial to note that the number of dimensions correlates with the number of variables necessary to specify a specific point on an object. While all three-dimensional objects have three dimensions for rotation, considering rotation on a plane implies the existence of six rotational axes: XY, YZ, XZ, XW, YW, and ZW.

A phenomenon known as "Hyper Rotation" occurs when a 3D object rotates, and its projection faces a 2D surface, creating an appearance akin to a square moving back and forth. Similarly, 4D objects like the tesseract produce a similar effect, manifesting as a trapezoid when facing a 3D space.

However, our inability to comprehend the fourth dimension does not impede mathematical operations involving it. Just as the Pythagorean theorem operates in 3D, the same formula, with slight modifications, applies to 4D:

Fifth dimension is considered to be micro-dimension and it is accepted in physics and mathematics. It is thought to be unobservable due to being very small.

The fifth dimension is regarded as a micro-dimension accepted within physics and mathematics. However, it is considered unobservable due to its infinitesimal nature.

Our world is perceived as 3D, yet due to the time taken for light to travel to our eyes, we observe the world in a 2D manner in everyday life. Consequently, seeing the fifth dimension is deemed impossible for humans. Nevertheless, the fifth dimension holds significant importance in physics and mathematics.

In physics, the fifth dimension is believed to unify electromagnetic and gravitational forces into a single force. This hypothesis stems from the Kaluza-Klein theory, paving the way for the creation of "String theory," primarily attributed to Italian physicist Gabriele Veneziano. This theory posits that the universe comprises minuscule vibrating strings, with phenomena like gravity resulting from the movements and vibrations of these strings. Presently, the fifth dimension is recognized as part of "string theory." Scientists anticipate that experiments conducted using the Large Hadron Collider may yield new evidence pertaining to the fifth dimension.

Despite numerous theories regarding the fifth dimension, scientists acknowledge its immense significance. They believe that deeper comprehension of this dimension could provide substantial insights into fundamental forces' nature and intricate mathematical relationships.

In summary, exploring dimensions reveals a captivating world beyond what we normally perceive. From understanding two-dimensional space as a base for shapes and visuals to living in a three-dimensional reality, our ability to grasp dimensions stops at the third due to how we see things.

Even though theories speculate about higher dimensions like the fourth or the tiny fifth, our inability to perceive beyond three dimensions is a hurdle. But in math, physics, and theories like string theory, we go beyond our limits, imagining these higher dimensions. These dimensions hold clues about how forces could come together and complex math connections.

The mystery of higher dimensions keeps us curious, pushing scientists to dig deeper, looking for answers that might unlock the secrets of our universe.

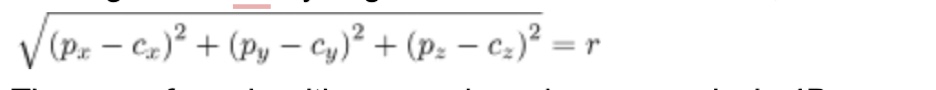
However, our inability to comprehend the fourth dimension does not impede mathematical operations involving it. Just as the Pythagorean theorem operates in 3D, the same formula, with slight modifications, applies to 4D:

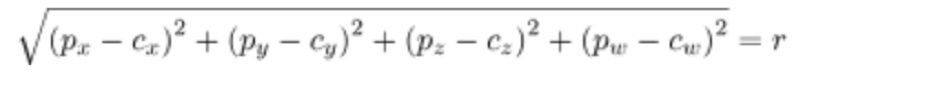
The fifth dimension is regarded as a micro-dimension accepted within physics and mathematics. However, it is considered unobservable due to its infinitesimal nature.

Our world is perceived as 3D, yet due to the time taken for light to travel to our eyes, we observe the world in a 2D manner in everyday life. Consequently, seeing the fifth dimension is deemed impossible for humans. Nevertheless, the fifth dimension holds significant importance in physics and mathematics.

In physics, the fifth dimension is believed to unify electromagnetic and gravitational forces into a single force. This hypothesis stems from the Kaluza-Klein theory, paving the way for the creation of "String theory," primarily attributed to Italian physicist Gabriele Veneziano. This theory posits that the universe comprises minuscule vibrating strings, with phenomena like gravity resulting from the movements and vibrations of these strings. Presently, the fifth dimension is recognized as part of "string theory." Scientists anticipate that experiments conducted using the Large Hadron Collider may yield new evidence pertaining to the fifth dimension.

Despite numerous theories regarding the fifth dimension, scientists acknowledge its immense significance. They believe that deeper comprehension of this dimension could provide substantial insights into fundamental forces' nature and intricate mathematical relationships.

In summary, exploring dimensions reveals a captivating world beyond what we normally perceive. From understanding two-dimensional space as a base for shapes and visuals to living in a three-dimensional reality, our ability to grasp dimensions stops at the third due to how we see things.

Even though theories speculate about higher dimensions like the fourth or the tiny fifth, our inability to perceive beyond three dimensions is a hurdle. But in math, physics, and theories like string theory, we go beyond our limits, imagining these higher dimensions. These dimensions hold clues about how forces could come together and complex math connections.

The mystery of higher dimensions keeps us curious, pushing scientists to dig deeper, looking for answers that might unlock the secrets of our universe.